class: left, middle, inverse background-image: url(img/portada.jpg) background-size: cover <div style="left: 0; width: 60%; padding; 0"> <!-- <div style=""> --> <img src="https://mounabelaid.netlify.app/post/r-ladies-tunis-meetups/featured.png" height="110px" style="padding-left: 20%"/> <img src="https://github.com/easystats/report/blob/master/man/figures/logo.png?raw=true" height="100px"/> <!-- <div/> --> # Reportando resultados estadísticos con `report` ## **R-Ladies Cuernavaca** ### Carlos A. Torres Cubilla ### 6 de mayo de 2021 <div/> --- class: inverse, middle, center <!-- <div class="my-logo-left"></div> --> # Sobre mí <img style="border-radius: 50%;" src="img/avatar.png" width="150px"/> ## Carlos Torres 🇵🇦 ### Cietífico de Datos en <a href="https://www.bgeneral.com/">Banco General</a> [<i class="fa fa-link" role="presentation" aria-label="link icon"></i> carlostorrescubila.github.io](https://carlostorrescubila.github.io/) &ensp; [<i class="fab fa-twitter" role="presentation" aria-label="twitter icon"></i> @carlos_tc22](https://twitter.com/carlos_tc22) &ensp; [<i class="fab fa-github" role="presentation" aria-label="github icon"></i> @carlostorrescubila](https://github.com/carlostorrescubila) --- class: inverse, center, middle # Get Started <img src="https://media4.giphy.com/media/PZcsDneMCLF65uxJuX/200w.webp?cid=ecf05e47vv92p8vn8z8sv26krwswe4jqpr2xfwo5126bey49&rid=200w.webp" width="50%"> --- class: center # `report`: “From R to your manuscript” <a href="https://easystats.github.io/report/"> <img src="https://github.com/easystats/report/blob/master/man/figures/logo.png?raw=true" width="50%"> </a> --- # ¿Qué es `report`? ¿Para qué sirve? `report` es un paquete en lenguaje R perteneciente al grupo de paquetes conocido como [`easystats`](https://easystats.github.io/easystats/). El objetivo principal de `report` es cerrar la brecha entre la salida de R y los resultados estructurados contenidos en un manuscrito. Este genera automáticamente informes de modelos y *dataframes* de acuerdo con las pautas de las mejores prácticas (por ejemplo, el estilo de la [APA](https://apastyle.apa.org/)), lo que garantiza la estandarización y la calidad al informar resultados. -- Este es un paquete joven y en continuo desarrollo. Fue publicado en [GitHub](https://github.com/easystats/report) el 29 de octubre de 2020 (version 0.0.1) y actualmente se encuentra en su versión 0.2.0. Sus desarrolladores invitan la comunidad a colaborar en el desarrollo del paquete respetando la guía de contribuciones que puede encontrar [AQUÍ](https://github.com/easystats/report/blob/master/.github/CONTRIBUTING.md) -- ## Instalación ```r install.packages("remotes") remotes::install_github("easystats/report") # No está en CRAN ``` --- # Flujo de trabajo 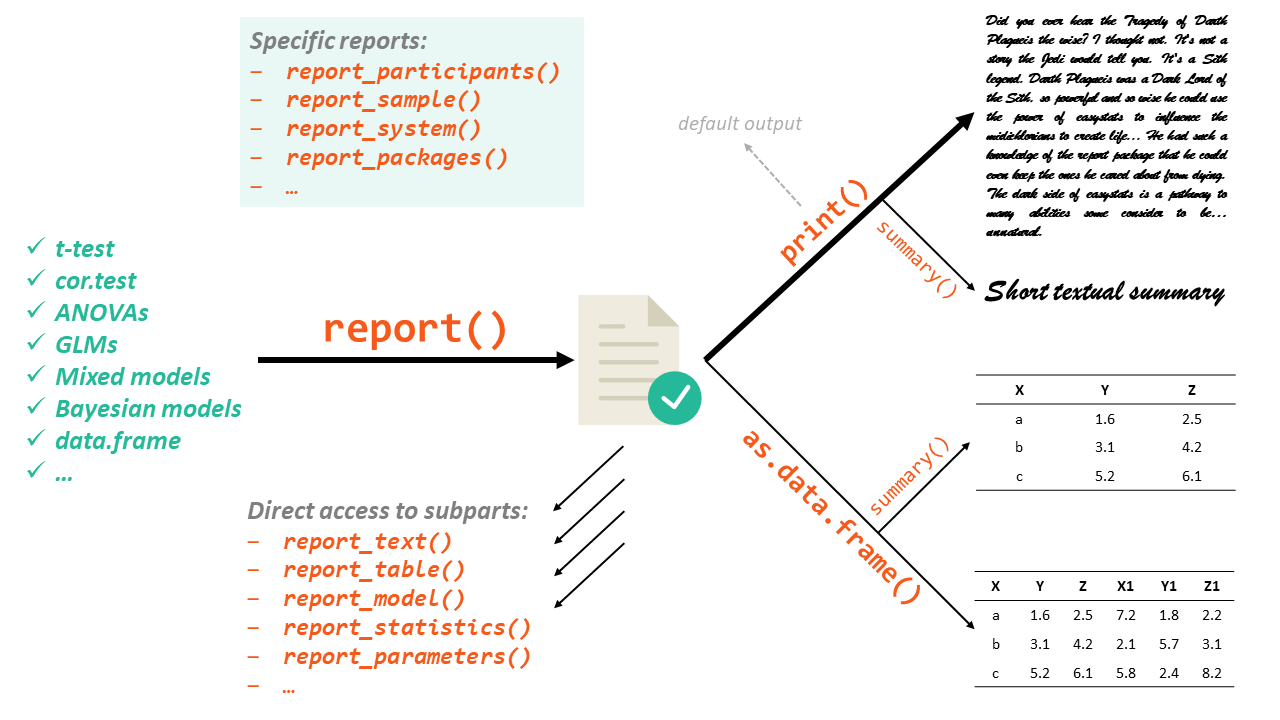 --- # Cargar paquetes ```r library(dplyr) *library(report) library(palmerpenguins) ``` -- <br><br> .center[ <a href="https://dplyr.tidyverse.org/"> <img src="https://d33wubrfki0l68.cloudfront.net/621a9c8c5d7b47c4b6d72e8f01f28d14310e8370/193fc/css/images/hex/dplyr.png" width="25%"> </a> <a href="https://easystats.github.io/report/"> <img src="https://github.com/easystats/report/blob/master/man/figures/logo.png?raw=true" width="25%"> </a> <a href="https://allisonhorst.github.io/palmerpenguins/"> <img src="https://allisonhorst.github.io/palmerpenguins/man/figures/palmerpenguins.png" width="25%"> </a> ] --- # Datos utilizados: `penguins` Los datos fueron recopilados y puestos a disposición por la [Dra. Kristen Gorman](https://www.uaf.edu/cfos/people/faculty/detail/kristen-gorman.php) y la [Palmer Station Antarctica LTER](https://pal.lternet.edu/), miembro de la [Red de Investigación Ecológica a Largo Plazo](https://lternet.edu/). -- .center[ <img src="https://allisonhorst.github.io/palmerpenguins/reference/figures/lter_penguins.png" width="80%"> ] --- # Datos utilizados: `penguins` <div id="htmlwidget-978baaef13e0db35664d" style="width:100%;height:auto;" class="datatables html-widget"></div> <script type="application/json" data-for="htmlwidget-978baaef13e0db35664d">{"x":{"filter":"none","data":[["1","2","3","4","5","6","7","8","9","10","11","12","13","14","15","16","17","18","19","20","21","22","23","24","25","26","27","28","29","30","31","32","33","34","35","36","37","38","39","40","41","42","43","44","45","46","47","48","49","50","51","52","53","54","55","56","57","58","59","60","61","62","63","64","65","66","67","68","69","70","71","72","73","74","75","76","77","78","79","80","81","82","83","84","85","86","87","88","89","90","91","92","93","94","95","96","97","98","99","100","101","102","103","104","105","106","107","108","109","110","111","112","113","114","115","116","117","118","119","120","121","122","123","124","125","126","127","128","129","130","131","132","133","134","135","136","137","138","139","140","141","142","143","144","145","146","147","148","149","150","151","152","153","154","155","156","157","158","159","160","161","162","163","164","165","166","167","168","169","170","171","172","173","174","175","176","177","178","179","180","181","182","183","184","185","186","187","188","189","190","191","192","193","194","195","196","197","198","199","200","201","202","203","204","205","206","207","208","209","210","211","212","213","214","215","216","217","218","219","220","221","222","223","224","225","226","227","228","229","230","231","232","233","234","235","236","237","238","239","240","241","242","243","244","245","246","247","248","249","250","251","252","253","254","255","256","257","258","259","260","261","262","263","264","265","266","267","268","269","270","271","272","273","274","275","276","277","278","279","280","281","282","283","284","285","286","287","288","289","290","291","292","293","294","295","296","297","298","299","300","301","302","303","304","305","306","307","308","309","310","311","312","313","314","315","316","317","318","319","320","321","322","323","324","325","326","327","328","329","330","331","332","333","334","335","336","337","338","339","340","341","342","343","344"],["Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Adelie","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Gentoo","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap","Chinstrap"],["Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Torgersen","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Biscoe","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream","Dream"],[39.1,39.5,40.3,null,36.7,39.3,38.9,39.2,34.1,42,37.8,37.8,41.1,38.6,34.6,36.6,38.7,42.5,34.4,46,37.8,37.7,35.9,38.2,38.8,35.3,40.6,40.5,37.9,40.5,39.5,37.2,39.5,40.9,36.4,39.2,38.8,42.2,37.6,39.8,36.5,40.8,36,44.1,37,39.6,41.1,37.5,36,42.3,39.6,40.1,35,42,34.5,41.4,39,40.6,36.5,37.6,35.7,41.3,37.6,41.1,36.4,41.6,35.5,41.1,35.9,41.8,33.5,39.7,39.6,45.8,35.5,42.8,40.9,37.2,36.2,42.1,34.6,42.9,36.7,35.1,37.3,41.3,36.3,36.9,38.3,38.9,35.7,41.1,34,39.6,36.2,40.8,38.1,40.3,33.1,43.2,35,41,37.7,37.8,37.9,39.7,38.6,38.2,38.1,43.2,38.1,45.6,39.7,42.2,39.6,42.7,38.6,37.3,35.7,41.1,36.2,37.7,40.2,41.4,35.2,40.6,38.8,41.5,39,44.1,38.5,43.1,36.8,37.5,38.1,41.1,35.6,40.2,37,39.7,40.2,40.6,32.1,40.7,37.3,39,39.2,36.6,36,37.8,36,41.5,46.1,50,48.7,50,47.6,46.5,45.4,46.7,43.3,46.8,40.9,49,45.5,48.4,45.8,49.3,42,49.2,46.2,48.7,50.2,45.1,46.5,46.3,42.9,46.1,44.5,47.8,48.2,50,47.3,42.8,45.1,59.6,49.1,48.4,42.6,44.4,44,48.7,42.7,49.6,45.3,49.6,50.5,43.6,45.5,50.5,44.9,45.2,46.6,48.5,45.1,50.1,46.5,45,43.8,45.5,43.2,50.4,45.3,46.2,45.7,54.3,45.8,49.8,46.2,49.5,43.5,50.7,47.7,46.4,48.2,46.5,46.4,48.6,47.5,51.1,45.2,45.2,49.1,52.5,47.4,50,44.9,50.8,43.4,51.3,47.5,52.1,47.5,52.2,45.5,49.5,44.5,50.8,49.4,46.9,48.4,51.1,48.5,55.9,47.2,49.1,47.3,46.8,41.7,53.4,43.3,48.1,50.5,49.8,43.5,51.5,46.2,55.1,44.5,48.8,47.2,null,46.8,50.4,45.2,49.9,46.5,50,51.3,45.4,52.7,45.2,46.1,51.3,46,51.3,46.6,51.7,47,52,45.9,50.5,50.3,58,46.4,49.2,42.4,48.5,43.2,50.6,46.7,52,50.5,49.5,46.4,52.8,40.9,54.2,42.5,51,49.7,47.5,47.6,52,46.9,53.5,49,46.2,50.9,45.5,50.9,50.8,50.1,49,51.5,49.8,48.1,51.4,45.7,50.7,42.5,52.2,45.2,49.3,50.2,45.6,51.9,46.8,45.7,55.8,43.5,49.6,50.8,50.2],[18.7,17.4,18,null,19.3,20.6,17.8,19.6,18.1,20.2,17.1,17.3,17.6,21.2,21.1,17.8,19,20.7,18.4,21.5,18.3,18.7,19.2,18.1,17.2,18.9,18.6,17.9,18.6,18.9,16.7,18.1,17.8,18.9,17,21.1,20,18.5,19.3,19.1,18,18.4,18.5,19.7,16.9,18.8,19,18.9,17.9,21.2,17.7,18.9,17.9,19.5,18.1,18.6,17.5,18.8,16.6,19.1,16.9,21.1,17,18.2,17.1,18,16.2,19.1,16.6,19.4,19,18.4,17.2,18.9,17.5,18.5,16.8,19.4,16.1,19.1,17.2,17.6,18.8,19.4,17.8,20.3,19.5,18.6,19.2,18.8,18,18.1,17.1,18.1,17.3,18.9,18.6,18.5,16.1,18.5,17.9,20,16,20,18.6,18.9,17.2,20,17,19,16.5,20.3,17.7,19.5,20.7,18.3,17,20.5,17,18.6,17.2,19.8,17,18.5,15.9,19,17.6,18.3,17.1,18,17.9,19.2,18.5,18.5,17.6,17.5,17.5,20.1,16.5,17.9,17.1,17.2,15.5,17,16.8,18.7,18.6,18.4,17.8,18.1,17.1,18.5,13.2,16.3,14.1,15.2,14.5,13.5,14.6,15.3,13.4,15.4,13.7,16.1,13.7,14.6,14.6,15.7,13.5,15.2,14.5,15.1,14.3,14.5,14.5,15.8,13.1,15.1,14.3,15,14.3,15.3,15.3,14.2,14.5,17,14.8,16.3,13.7,17.3,13.6,15.7,13.7,16,13.7,15,15.9,13.9,13.9,15.9,13.3,15.8,14.2,14.1,14.4,15,14.4,15.4,13.9,15,14.5,15.3,13.8,14.9,13.9,15.7,14.2,16.8,14.4,16.2,14.2,15,15,15.6,15.6,14.8,15,16,14.2,16.3,13.8,16.4,14.5,15.6,14.6,15.9,13.8,17.3,14.4,14.2,14,17,15,17.1,14.5,16.1,14.7,15.7,15.8,14.6,14.4,16.5,15,17,15.5,15,13.8,16.1,14.7,15.8,14,15.1,15.2,15.9,15.2,16.3,14.1,16,15.7,16.2,13.7,null,14.3,15.7,14.8,16.1,17.9,19.5,19.2,18.7,19.8,17.8,18.2,18.2,18.9,19.9,17.8,20.3,17.3,18.1,17.1,19.6,20,17.8,18.6,18.2,17.3,17.5,16.6,19.4,17.9,19,18.4,19,17.8,20,16.6,20.8,16.7,18.8,18.6,16.8,18.3,20.7,16.6,19.9,19.5,17.5,19.1,17,17.9,18.5,17.9,19.6,18.7,17.3,16.4,19,17.3,19.7,17.3,18.8,16.6,19.9,18.8,19.4,19.5,16.5,17,19.8,18.1,18.2,19,18.7],[181,186,195,null,193,190,181,195,193,190,186,180,182,191,198,185,195,197,184,194,174,180,189,185,180,187,183,187,172,180,178,178,188,184,195,196,190,180,181,184,182,195,186,196,185,190,182,179,190,191,186,188,190,200,187,191,186,193,181,194,185,195,185,192,184,192,195,188,190,198,190,190,196,197,190,195,191,184,187,195,189,196,187,193,191,194,190,189,189,190,202,205,185,186,187,208,190,196,178,192,192,203,183,190,193,184,199,190,181,197,198,191,193,197,191,196,188,199,189,189,187,198,176,202,186,199,191,195,191,210,190,197,193,199,187,190,191,200,185,193,193,187,188,190,192,185,190,184,195,193,187,201,211,230,210,218,215,210,211,219,209,215,214,216,214,213,210,217,210,221,209,222,218,215,213,215,215,215,216,215,210,220,222,209,207,230,220,220,213,219,208,208,208,225,210,216,222,217,210,225,213,215,210,220,210,225,217,220,208,220,208,224,208,221,214,231,219,230,214,229,220,223,216,221,221,217,216,230,209,220,215,223,212,221,212,224,212,228,218,218,212,230,218,228,212,224,214,226,216,222,203,225,219,228,215,228,216,215,210,219,208,209,216,229,213,230,217,230,217,222,214,null,215,222,212,213,192,196,193,188,197,198,178,197,195,198,193,194,185,201,190,201,197,181,190,195,181,191,187,193,195,197,200,200,191,205,187,201,187,203,195,199,195,210,192,205,210,187,196,196,196,201,190,212,187,198,199,201,193,203,187,197,191,203,202,194,206,189,195,207,202,193,210,198],[3750,3800,3250,null,3450,3650,3625,4675,3475,4250,3300,3700,3200,3800,4400,3700,3450,4500,3325,4200,3400,3600,3800,3950,3800,3800,3550,3200,3150,3950,3250,3900,3300,3900,3325,4150,3950,3550,3300,4650,3150,3900,3100,4400,3000,4600,3425,2975,3450,4150,3500,4300,3450,4050,2900,3700,3550,3800,2850,3750,3150,4400,3600,4050,2850,3950,3350,4100,3050,4450,3600,3900,3550,4150,3700,4250,3700,3900,3550,4000,3200,4700,3800,4200,3350,3550,3800,3500,3950,3600,3550,4300,3400,4450,3300,4300,3700,4350,2900,4100,3725,4725,3075,4250,2925,3550,3750,3900,3175,4775,3825,4600,3200,4275,3900,4075,2900,3775,3350,3325,3150,3500,3450,3875,3050,4000,3275,4300,3050,4000,3325,3500,3500,4475,3425,3900,3175,3975,3400,4250,3400,3475,3050,3725,3000,3650,4250,3475,3450,3750,3700,4000,4500,5700,4450,5700,5400,4550,4800,5200,4400,5150,4650,5550,4650,5850,4200,5850,4150,6300,4800,5350,5700,5000,4400,5050,5000,5100,4100,5650,4600,5550,5250,4700,5050,6050,5150,5400,4950,5250,4350,5350,3950,5700,4300,4750,5550,4900,4200,5400,5100,5300,4850,5300,4400,5000,4900,5050,4300,5000,4450,5550,4200,5300,4400,5650,4700,5700,4650,5800,4700,5550,4750,5000,5100,5200,4700,5800,4600,6000,4750,5950,4625,5450,4725,5350,4750,5600,4600,5300,4875,5550,4950,5400,4750,5650,4850,5200,4925,4875,4625,5250,4850,5600,4975,5500,4725,5500,4700,5500,4575,5500,5000,5950,4650,5500,4375,5850,4875,6000,4925,null,4850,5750,5200,5400,3500,3900,3650,3525,3725,3950,3250,3750,4150,3700,3800,3775,3700,4050,3575,4050,3300,3700,3450,4400,3600,3400,2900,3800,3300,4150,3400,3800,3700,4550,3200,4300,3350,4100,3600,3900,3850,4800,2700,4500,3950,3650,3550,3500,3675,4450,3400,4300,3250,3675,3325,3950,3600,4050,3350,3450,3250,4050,3800,3525,3950,3650,3650,4000,3400,3775,4100,3775],["male","female","female",null,"female","male","female","male",null,null,null,null,"female","male","male","female","female","male","female","male","female","male","female","male","male","female","male","female","female","male","female","male","female","male","female","male","male","female","female","male","female","male","female","male","female","male","male",null,"female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","male","female","male","female","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","male","female","female","male","female","male","female","male","female","male","male","female","female","male","female","male","female","male","female","male","female","male","female","male","female","male","male","female","female","male","female","male",null,"male","female","male","male","female","female","male","female","male","female","male","female","male","female","male","female","male","male","female","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male",null,"male","female","male","female","male","male","female","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","male","female","female","male","female","male","female","male",null,"male","female","male","female","male","female","male","female","male","female","male",null,"male","female",null,"female","male","female","male","female","male","male","female","male","female","female","male","female","male","female","male","female","male","female","male","male","female","female","male","female","male","female","male","female","male","female","male","female","male","female","male","female","male","male","female","female","male","female","male","male","female","male","female","female","male","female","male","male","female","female","male","female","male","female","male","female","male","male","female","male","female","female","male","female","male","male","female"],[2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2007,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2008,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009,2009]],"container":"<table class=\"cell-border stripe\">\n <thead>\n <tr>\n <th> <\/th>\n <th>species<\/th>\n <th>island<\/th>\n <th>bill_length_mm<\/th>\n <th>bill_depth_mm<\/th>\n <th>flipper_length_mm<\/th>\n <th>body_mass_g<\/th>\n <th>sex<\/th>\n <th>year<\/th>\n <\/tr>\n <\/thead>\n<\/table>","options":{"pageLength":7,"scrollX":true,"columnDefs":[{"className":"dt-right","targets":[3,4,5,6,8]},{"orderable":false,"targets":0}],"order":[],"autoWidth":false,"orderClasses":false,"lengthMenu":[7,10,25,50,100]}},"evals":[],"jsHooks":[]}</script> --- # Datos utilizados: `penguins` .center[ <img src="https://raw.githubusercontent.com/allisonhorst/palmerpenguins/master/man/figures/culmen_depth.png" width="80%"> ] --- # Reportes específicos Las principales funciones que generan informes específicos que no están relacionados con métodos estadísticos son: - `report_system()` - `report_packages()` - `cite_packages()` - `report_date()` - `report_participants()` - `report_sample()` --- ## Informe del sistema ### Default ```r report_system() ``` ``` Analyses were conducted using the R Statistical language (version 4.0.5; R Core Team, 2021) on Windows 10 x64 (build 19041) ``` ### Summary ```r report_system() %>% summary() ``` ``` The analysis was done using the R Statistical language (v4.0.5; R Core Team, 2021) on Windows 10 x64 ``` --- ## Informe de paquetes ### Default ```r report_packages() ``` ``` - metathis (version 1.0.3; Garrick Aden-Buie, 2020) - dplyr (version 1.0.5; Hadley Wickham et al., 2021) - palmerpenguins (version 0.1.0; Horst AM et al., 2020) - report (version 0.3.0.9000; Makowski et al., 2020) - R (version 4.0.5; R Core Team, 2021) ``` ### Summary ```r report_packages() %>% summary() ``` ``` - metathis (v1.0.3) - dplyr (v1.0.5) - palmerpenguins (v0.1.0) - report (v0.3.0.9000) - R (v4.0.5) ``` --- ## Citar paquetes .panelset[ .panel[.panel-name[R base] ```r citation("dplyr") ``` ``` To cite package 'dplyr' in publications use: Hadley Wickham, Romain François, Lionel Henry and Kirill Müller (2021). dplyr: A Grammar of Data Manipulation. R package version 1.0.5. https://CRAN.R-project.org/package=dplyr A BibTeX entry for LaTeX users is @Manual{, title = {dplyr: A Grammar of Data Manipulation}, author = {Hadley Wickham and Romain François and Lionel Henry and Kirill Müller}, year = {2021}, note = {R package version 1.0.5}, url = {https://CRAN.R-project.org/package=dplyr}, } ``` ] .panel[.panel-name[report] #### Para las referencias ```r cite_packages() ``` ``` - Garrick Aden-Buie (2020). metathis: HTML Metadata Tags for 'R Markdown' and 'Shiny'. R package version 1.0.3. https://CRAN.R-project.org/package=metathis - Hadley Wickham, Romain François, Lionel Henry and Kirill Müller (2021). dplyr: A Grammar of Data Manipulation. R package version 1.0.5. https://CRAN.R-project.org/package=dplyr - Horst AM, Hill AP, Gorman KB (2020). palmerpenguins: Palmer Archipelago (Antarctica) penguin data. R package version 0.1.0. https://allisonhorst.github.io/palmerpenguins/ - Makowski, D., Ben-Shachar, M.S., Patil, I. & Lüdecke, D. (2020). Automated Results Reporting as a Practical Tool to Improve Reproducibility and Methodological Best Practices Adoption. CRAN. Available from https://github.com/easystats/report. doi: . - R Core Team (2021). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/. ``` #### Para las citas ```r cite_packages() %>% format_citation(authorsdate = TRUE, short = TRUE, intext = FALSE) ``` ``` - Garrick Aden-Buie (2020) - Hadley Wickham et al. (2021) - Horst AM et al. (2020) - Makowski et al. (2020) - R Core Team (2021) ``` ] .panel[.panel-name[report 2] ```r report(sessionInfo()) ``` ``` Analyses were conducted using the R Statistical language (version 4.0.5; R Core Team, 2021) on Windows 10 x64 (build 19041), using the packages metathis (version 1.0.3; Garrick Aden-Buie, 2020), dplyr (version 1.0.5; Hadley Wickham et al., 2021), palmerpenguins (version 0.1.0; Horst AM et al., 2020) and report (version 0.3.0.9000; Makowski et al., 2020). References ---------- - Garrick Aden-Buie (2020). metathis: HTML Metadata Tags for 'R Markdown' and 'Shiny'. R package version 1.0.3. https://CRAN.R-project.org/package=metathis - Hadley Wickham, Romain François, Lionel Henry and Kirill Müller (2021). dplyr: A Grammar of Data Manipulation. R package version 1.0.5. https://CRAN.R-project.org/package=dplyr - Horst AM, Hill AP, Gorman KB (2020). palmerpenguins: Palmer Archipelago (Antarctica) penguin data. R package version 0.1.0. https://allisonhorst.github.io/palmerpenguins/ - Makowski, D., Ben-Shachar, M.S., Patil, I. & Lüdecke, D. (2020). Automated Results Reporting as a Practical Tool to Improve Reproducibility and Methodological Best Practices Adoption. CRAN. Available from https://github.com/easystats/report. doi: . - R Core Team (2021). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/. ``` ] ] --- ## Informe de fecha ### Default ```r report_date() ``` ``` It's jueves, mayo 06 of the year 2021, at 6p.m. 07 and 35 seconds ``` ### Summary ```r report_date() %>% summary() ``` ``` 06/05/21 - 18:07:35 ``` --- ## Informe de participantes (Datos) ```r Participantes <- data.frame( "Edad" = c(22, 22, 54, 34, 18, 28, 42, 45), "Genero" = c("F", "M", "F", "M", "F", "M", "F", "M"), "Años_Experiencia" = c(1, 2, 24, 9, 0, 5, 12, 20), "Nivel_Educacion" = c("Highschool", "Bachelor", "PhD", "Bachelor", "Highschool", "Bachelor", "Bachelor", "PhD"), "Grupo" = c("A", "A", "A", "A", "B", "B", "B", "B") ) ``` <div id="htmlwidget-fdc6d9174f29950783e7" style="width:100%;height:auto;" class="datatables html-widget"></div> <script type="application/json" data-for="htmlwidget-fdc6d9174f29950783e7">{"x":{"filter":"none","data":[["1","2","3","4","5","6","7","8"],[22,22,54,34,18,28,42,45],["F","M","F","M","F","M","F","M"],[1,2,24,9,0,5,12,20],["Highschool","Bachelor","PhD","Bachelor","Highschool","Bachelor","Bachelor","PhD"],["A","A","A","A","B","B","B","B"]],"container":"<table class=\"cell-border stripe\">\n <thead>\n <tr>\n <th> <\/th>\n <th>Edad<\/th>\n <th>Genero<\/th>\n <th>Años_Experiencia<\/th>\n <th>Nivel_Educacion<\/th>\n <th>Grupo<\/th>\n <\/tr>\n <\/thead>\n<\/table>","options":{"pageLength":4,"columnDefs":[{"className":"dt-right","targets":[1,3]},{"orderable":false,"targets":0}],"order":[],"autoWidth":false,"orderClasses":false,"lengthMenu":[4,10,25,50,100]}},"evals":[],"jsHooks":[]}</script> --- ## Informe de participantes .panelset[ .panel[.panel-name[Edad y género] ```r report_participants( Participantes, age = "Edad", sex = "Genero" ) ``` ``` [1] "8 participants (Mean age = 33.1, SD = 12.9, range: [18, 54]; 50.0% females)" ``` ] .panel[.panel-name[Años de educación] ```r report_participants( Participantes, age = "Edad", sex = "Genero", education = "Años_Experiencia" ) ``` ``` [1] "8 participants (Mean age = 33.1, SD = 12.9, range: [18, 54]; 50.0% females; Mean education = 9.1, SD = 9.0, range: [0, 24])" ``` ] .panel[.panel-name[Nivel de eduación] ```r report_participants( Participantes, age = "Edad", sex = "Genero", education = "Nivel_Educacion" ) ``` ``` [1] "8 participants (Mean age = 33.1, SD = 12.9, range: [18, 54]; 50.0% females; Education: Bachelor, 50.00%; Highschool, 25.00%; PhD, 25.00%)" ``` ] .panel[.panel-name[Por grupo] ```r report_participants( Participantes, age = "Edad", sex = "Genero", group = "Grupo" ) ``` ``` [1] "For the 'Grupo - A' group: 4 participants (Mean age = 33.0, SD = 15.1, range: [22, 54]; 50.0% females) and for the 'Grupo - B' group: 4 participants (Mean age = 33.2, SD = 12.6, range: [18, 45]; 50.0% females)" ``` ] ] --- ## Informe de muestra .panelset[ .panel[.panel-name[Default] ```r report_sample(penguins) ``` ``` # Descriptive Statistics Variable | Summary ---------------------------------------------- species [Adelie], % | 44.2 species [Chinstrap], % | 19.8 species [Gentoo], % | 36.0 island [Biscoe], % | 48.8 island [Dream], % | 36.0 island [Torgersen], % | 15.1 Mean bill_length_mm (SD) | 43.92 (5.46) Mean bill_depth_mm (SD) | 17.15 (1.97) Mean flipper_length_mm (SD) | 200.92 (14.06) Mean body_mass_g (SD) | 4201.75 (801.95) sex [male], % | 50.5 Mean year (SD) | 2008.03 (0.82) ``` ] .panel[.panel-name[Por grupo] ```r report_sample(penguins, group_by = "species") ``` ``` # Descriptive Statistics Variable | Adelie (n=152) | Chinstrap (n=68) | Gentoo (n=124) | Total ------------------------------------------------------------------------------------------------------- island [Biscoe], % | 28.9 | 0.0 | 100.0 | 48.8 island [Dream], % | 36.8 | 100.0 | 0.0 | 36.0 island [Torgersen], % | 34.2 | 0.0 | 0.0 | 15.1 Mean bill_length_mm (SD) | 38.79 (2.66) | 48.83 (3.34) | 47.50 (3.08) | 43.92 (5.46) Mean bill_depth_mm (SD) | 18.35 (1.22) | 18.42 (1.14) | 14.98 (0.98) | 17.15 (1.97) Mean flipper_length_mm (SD) | 189.95 (6.54) | 195.82 (7.13) | 217.19 (6.48) | 200.92 (14.06) Mean body_mass_g (SD) | 3700.66 (458.57) | 3733.09 (384.34) | 5076.02 (504.12) | 4201.75 (801.95) sex [male], % | 50.0 | 50.0 | 51.3 | 50.5 Mean year (SD) | 2008.01 (0.82) | 2007.97 (0.86) | 2008.08 (0.79) | 2008.03 (0.82) ``` ] .panel[.panel-name[Seleccionando columnas] ```r report_sample( penguins, group_by = "species", select = c("species", "sex", "bill_length_mm", "bill_depth_mm") ) ``` ``` # Descriptive Statistics Variable | Adelie (n=152) | Chinstrap (n=68) | Gentoo (n=124) | Total -------------------------------------------------------------------------------------------- sex [male], % | 50.0 | 50.0 | 51.3 | 50.5 Mean bill_length_mm (SD) | 38.79 (2.66) | 48.83 (3.34) | 47.50 (3.08) | 43.92 (5.46) Mean bill_depth_mm (SD) | 18.35 (1.22) | 18.42 (1.14) | 14.98 (0.98) | 17.15 (1.97) ``` ] .panel[.panel-name[Excluyendo columnas] ```r report_sample( penguins, group_by = "species", exclude = c("island", "flipper_length_mm", "body_mass_g", "year") ) ``` ``` # Descriptive Statistics Variable | Adelie (n=152) | Chinstrap (n=68) | Gentoo (n=124) | Total -------------------------------------------------------------------------------------------- Mean bill_length_mm (SD) | 38.79 (2.66) | 48.83 (3.34) | 47.50 (3.08) | 43.92 (5.46) Mean bill_depth_mm (SD) | 18.35 (1.22) | 18.42 (1.14) | 14.98 (0.98) | 17.15 (1.97) sex [male], % | 50.0 | 50.0 | 51.3 | 50.5 ``` ] ] --- class: inverse, center, middle # Informe de un data frame --- # Informe de un data frame .panelset[ .panel[.panel-name[Default] ```r report(penguins) ``` ``` The data contains 344 observations of the following 8 variables: - species: 3 levels, namely Adelie (n = 152, 44.19%), Chinstrap (n = 68, 19.77%) and Gentoo (n = 124, 36.05%) - island: 3 levels, namely Biscoe (n = 168, 48.84%), Dream (n = 124, 36.05%) and Torgersen (n = 52, 15.12%) - bill_length_mm: n = 344, Mean = 43.92, SD = 5.46, Median = , MAD = 7.04, range: [32.10, 59.60], Skewness = 0.05, Kurtosis = -0.88, 0.58% missing - bill_depth_mm: n = 344, Mean = 17.15, SD = 1.97, Median = , MAD = 2.22, range: [13.10, 21.50], Skewness = -0.14, Kurtosis = -0.91, 0.58% missing - flipper_length_mm: n = 344, Mean = 200.92, SD = 14.06, Median = , MAD = 16.31, range: [172, 231], Skewness = 0.35, Kurtosis = -0.98, 0.58% missing - body_mass_g: n = 344, Mean = 4201.75, SD = 801.95, Median = , MAD = 889.56, range: [2700, 6300], Skewness = 0.47, Kurtosis = -0.72, 0.58% missing - sex: 2 levels, namely female (n = 165, 47.97%), male (n = 168, 48.84%) and missing (n = 11, 3.20%) - year: n = 344, Mean = 2008.03, SD = 0.82, Median = 2008.00, MAD = 1.48, range: [2007, 2009], Skewness = -0.05, Kurtosis = -1.50, 0% missing ``` ] .panel[.panel-name[Summary] ```r report(penguins) %>% summary() ``` ``` The data contains 344 observations of the following 8 variables: - species: 3 levels, namely Adelie (n = 152), Chinstrap (n = 68) and Gentoo (n = 124) - island: 3 levels, namely Biscoe (n = 168), Dream (n = 124) and Torgersen (n = 52) - bill_length_mm: Mean = 43.92, SD = 5.46, range: [32.10, 59.60], 0.58% missing - bill_depth_mm: Mean = 17.15, SD = 1.97, range: [13.10, 21.50], 0.58% missing - flipper_length_mm: Mean = 200.92, SD = 14.06, range: [172, 231], 0.58% missing - body_mass_g: Mean = 4201.75, SD = 801.95, range: [2700, 6300], 0.58% missing - sex: 2 levels, namely female (n = 165), male (n = 168) and missing (n = 11) - year: Mean = 2008.03, SD = 0.82, range: [2007, 2009] ``` ] .panel[.panel-name[Usando dplyr] ```r penguins %>% select(-ends_with("_mm")) %>% group_by(species) %>% report() %>% summary() ``` ``` The data contains 344 observations, grouped by species, of the following 5 variables: - Adelie (n = 152): - island: 3 levels, namely Biscoe (n = 44), Dream (n = 56) and Torgersen (n = 52) - body_mass_g: Mean = 3700.66, SD = 458.57, range: [2850, 4775], 0.66% missing - sex: 2 levels, namely female (n = 73), male (n = 73) and missing (n = 6) - year: Mean = 2008.01, SD = 0.82, range: [2007, 2009] - Chinstrap (n = 68): - island: 3 levels, namely Biscoe (n = 0), Dream (n = 68) and Torgersen (n = 0) - body_mass_g: Mean = 3733.09, SD = 384.34, range: [2700, 4800] - sex: 2 levels, namely female (n = 34) and male (n = 34) - year: Mean = 2007.97, SD = 0.86, range: [2007, 2009] - Gentoo (n = 124): - island: 3 levels, namely Biscoe (n = 124), Dream (n = 0) and Torgersen (n = 0) - body_mass_g: Mean = 5076.02, SD = 504.12, range: [3950, 6300], 0.81% missing - sex: 2 levels, namely female (n = 58), male (n = 61) and missing (n = 5) - year: Mean = 2008.08, SD = 0.79, range: [2007, 2009] ``` ] ] --- class: inverse, center, middle # Reportes estadísticos <img src="https://media4.giphy.com/media/LPrAK9rEedDwjtL1J0/200.webp?cid=ecf05e47ugwngg89cftjjdg4xtuqv8ydamdgunpg7w7794s5&rid=200.webp" width="50%"> --- # Reportes estadísticos Las técnicas estadísticas que son posibles reportar con `report` son: - <p style="color:#88398A">Test de asosiación<p/> - <p style="color:#88398A">Test t para diferencia de medias<p/> - <p style="color:#88398A">Modelos lineales<p/> - <p style="color:#88398A">ANOVAs<p/> - Modelos lineales generalizados - Modelos mixtos - Modelos bayesianos --- ## Test de asociación La prueba de asociación o correlación se utiliza para probar si la correlación (indicada `\(\rho\)`) entre 2 variables es significativamente distinta de 0 o no en la población. Existen diferentes métodos para realizar análisis de correlación y sus respectivos contrastes de hipótesis: + **Pearson:** es una prueba paramétrica que se utiliza para medir el grado de relación lineal entre variables cuantitativas. Para que la prueba pueda aplicarse las variables deben ser independientes y normalmente distribuidas. + **Spearman:** es una prueba no paramétrica que no conlleva ninguna suposición sobre la distribución de los datos. Es ideal cuando las variables son ordinales, de intervalo o de razón. + **Kendall:** es una prueba no paramétrica que se calcula a partir del número de pares concordantes y discordantes. Se utiliza como alternativa a la prueba de Pearson cuando los datos con los que está trabajando fallaron en al menos uno de los supuestos. También es una alternativa a la prueba de Spearman cuando el tamaño de la muestra es pequeño y tiene muchos rangos empatados. ### Hipótesis $$ `\begin{cases} H_0: \rho = 0\\ H_1: \rho \neq 0 \end{cases}` $$ --- ## Test de asociación .panelset[ .panel[.panel-name[R base] ```r cor.test( x = penguins$bill_length_mm, y = penguins$bill_depth_mm, method = "pearson" ) ``` ``` Pearson's product-moment correlation data: penguins$bill_length_mm and penguins$bill_depth_mm t = -4.4591, df = 340, p-value = 1.12e-05 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: -0.3328072 -0.1323004 sample estimates: cor -0.2350529 ``` ] .panel[.panel-name[report] ```r cor.test( x = penguins$bill_length_mm, y = penguins$bill_depth_mm, method = "pearson" ) %>% report() ``` ``` Effect sizes were labelled following Funder's (2019) recommendations. The Pearson's product-moment correlation between penguins$bill_length_mm and penguins$bill_depth_mm is negative, statistically significant, and medium (r = -0.24, 95% CI [-0.33, -0.13], t(340) = -4.46, p < .001) ``` ] .panel[.panel-name[report as table] ```r cor.test( x = penguins$bill_length_mm, y = penguins$bill_depth_mm, method = "pearson" ) %>% report() %>% as.data.frame() ``` ``` Parameter1 | Parameter2 | r | 95% CI | t(340) | p | Method ---------------------------------------------------------------------------------------------------------------------------------- penguins$bill_length_mm | penguins$bill_depth_mm | -0.24 | [-0.33, -0.13] | -4.46 | < .001 | Pearson's product-moment correlation ``` ] ] --- ## Diferencia de medias (t-test) La prueba de diferencia de medias es un test paramétrico que determina la igualdad de dos conjuntos de datos. Al elegir una prueba t, se deben considerar dos cosas: 1. **¿Prueba t de una muestra, dos muestras (independientes o pareadas)?** <br> Si la muestra se está comparando con un valor, entonces se realiza una prueba t de una muestra. Por el contrario, si se comparan dos grupos se realiza una prueba de dos muestras. Esta puede ser de dos poblaciones independientes o o de una misma población. 2. **¿Prueba t de una o dos colas?** <br> Si solo importa si las dos poblaciones son diferentes entre sí, se realiza una prueba t de dos colas. Por el contrario, si desea saber si la media de una población es mayor o menor que la otra, se realiza una prueba t de una cola. ### Hipóteis .panelset[ .panel[.panel-name[Una muestra] $$ `\begin{cases} H_0: \mu = \mu_{0} \\ H_1: \mu \neq \mu_{0} \end{cases}` $$ ] .panel[.panel-name[Dos muestras] $$ `\begin{cases} H_0: \mu_{1} = \mu_{2} \\ H_1: \mu_{1} \neq \mu_{2} \end{cases}` $$ ] ] --- ## Diferencia de medias (t-test) .panelset[ .panel[.panel-name[R base] ```r t.test( formula = body_mass_g ~ sex, data = penguins, paired = FALSE ) ``` ``` Welch Two Sample t-test data: body_mass_g by sex t = -8.5545, df = 323.9, p-value = 4.794e-16 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -840.5783 -526.2453 sample estimates: mean in group female mean in group male 3862.273 4545.685 ``` ] .panel[.panel-name[report] ```r t.test( formula = body_mass_g ~ sex, data = penguins, paired = FALSE ) %>% report() ``` ``` Effect sizes were labelled following Cohen's (1988) recommendations. The Welch Two Sample t-test testing the difference of body_mass_g by sex (mean in group female = 3862.27, mean in group male = 4545.68) suggests that the effect is positive, statistically significant, and large (difference = 683.41, 95% CI [-840.58, -526.25], t(323.90) = -8.55, p < .001; Cohen's d = -0.95, 95% CI [-1.18, -0.72]) ``` ] .panel[.panel-name[report as table] ```r t.test( formula = body_mass_g ~ sex, data = penguins, paired = FALSE ) %>% report() %>% as.data.frame() ``` ``` Parameter | Group | Mean_Group1 | Mean_Group2 | Difference | 95% CI | t(323.90) | p | Method | d | d CI --------------------------------------------------------------------------------------------------------------------------------------------------------- body_mass_g | sex | 3862.27 | 4545.68 | 683.41 | [-840.58, -526.25] | -8.55 | < .001 | Welch Two Sample t-test | -0.95 | [-1.18, -0.72] ``` ] ] --- ## Regresión lineal La regresión es una técnica que permite generar un modelo lineal en el que el valor de una variable dependiente `\((Y)\)` se determina a partir de un conjunto de `\(k\)` variables independientes `\((X_{1}, X_{2}, \dots, X_{k})\)`. Los modelos de regresión lineal siguen la siguiente ecuación: $$ Y = \beta_{0} + \beta_i X_i + \varepsilon; \quad i = 1, 2, \dots, k $$ Donde: + La parte sistemática o no aleatoria es: `\(\beta_{0} + \beta_{i} X_{i}\)` + La parte estocástica o aleatoria es: `\(\varepsilon_{i}\)` Ademas: + `\(Y\)` es la variable dependiente o variable respuesta. + `\(X_{i}\)` es la i-ésima variable independiente o predictora. + `\(\beta_{0}\)` es el intercepto, es decir, el valor de `\(Y\)` cuando todas las variables predictoras valen 0. + `\(\beta_{i}\)` es el incremento de la variable dependiente por cada unidad de `\(X_{i}\)`, manteniendo las demás variables constantes. Son conocidos como como coeficientes de regresión. + `\(\varepsilon\)` son los errores o residuales. --- ## Regresión lineal .panelset[ .panel[.panel-name[R base] ```r lm( data = penguins, formula = body_mass_g~bill_length_mm + bill_depth_mm ) %>% summary() ``` ``` Call: lm(formula = body_mass_g ~ bill_length_mm + bill_depth_mm, data = penguins) Residuals: Min 1Q Median 3Q Max -1804.61 -454.83 8.15 463.53 1544.82 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 3343.136 429.912 7.776 9.05e-14 *** bill_length_mm 75.281 5.971 12.608 < 2e-16 *** bill_depth_mm -142.723 16.507 -8.646 < 2e-16 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 585.1 on 339 degrees of freedom (2 observations deleted due to missingness) Multiple R-squared: 0.4708, Adjusted R-squared: 0.4677 F-statistic: 150.8 on 2 and 339 DF, p-value: < 2.2e-16 ``` ] .panel[.panel-name[report] ```r lm( data = penguins, formula = body_mass_g~bill_length_mm + bill_depth_mm ) %>% report() ``` ``` We fitted a linear model (estimated using OLS) to predict body_mass_g with bill_length_mm and bill_depth_mm (formula: body_mass_g ~ bill_length_mm + bill_depth_mm). The model explains a statistically significant and substantial proportion of variance (R2 = 0.47, F(2, 339) = 150.82, p < .001, adj. R2 = 0.47). The model's intercept, corresponding to bill_length_mm = 0 and bill_depth_mm = 0, is at 3343.14 (95% CI [2497.50, 4188.77], t(339) = 7.78, p < .001). Within this model: - The effect of bill_length_mm is statistically significant and positive (beta = 75.28, 95% CI [63.54, 87.03], t(339) = 12.61, p < .001; Std. beta = 0.51, 95% CI [0.43, 0.59]) - The effect of bill_depth_mm is statistically significant and negative (beta = -142.72, 95% CI [-175.19, -110.25], t(339) = -8.65, p < .001; Std. beta = -0.35, 95% CI [-0.43, -0.27]) Standardized parameters were obtained by fitting the model on a standardized version of the dataset. ``` ] .panel[.panel-name[report as table] ```r lm( data = penguins, formula = body_mass_g~bill_length_mm + bill_depth_mm ) %>% report() %>% as.data.frame() ``` ``` Parameter | Coefficient | 95% CI | t(339) | p | Std. Coef. | Std. Coef. 95% CI | Fit -------------------------------------------------------------------------------------------------------------- (Intercept) | 3343.14 | [2497.50, 4188.77] | 7.78 | < .001 | 6.15e-16 | [-0.08, 0.08] | bill_length_mm | 75.28 | [ 63.54, 87.03] | 12.61 | < .001 | 0.51 | [ 0.43, 0.59] | bill_depth_mm | -142.72 | [-175.19, -110.25] | -8.65 | < .001 | -0.35 | [-0.43, -0.27] | | | | | | | | AIC | | | | | | | 5333.82 BIC | | | | | | | 5349.16 R2 | | | | | | | 0.47 R2 (adj.) | | | | | | | 0.47 Sigma | | | | | | | 585.08 ``` ] ] --- ## ANOVA El Análisis de Varianza (ANOVA) es una técnica paramétrica que se utiliza cuando los datos no están pareados y se quiere estudiar si existen diferencias significativas entre las medias de una variable aleatoria continua en los diferentes niveles de otra variable cualitativa o factor. Esta diferencia entre medias se detecta a través del estudio de la varianza entre grupos y dentro de grupos como se muestra en la siguiente tabla: | F.V. | S.C. | g.l. | M.C. | Estadístico <br>de contraste | |:------------:|:------------:|:-----:|:-------------------------------------:|:-----------------------------------:| | Entre grupos | `\(SC_{inter}\)` | `\(I-1\)` | `\(MC_{inter} = \frac{SC_{inter}}{I-1}\)` | `\(F = \frac{MC_{inter}}{MC_{intra}}\)` | | Intra grupos | `\(SC_{intra}\)` | `\(N-I\)` | `\(MC_{intra} = \frac{SC_{intra}}{N-I}\)` | | | Total | `\(SC_{total}\)` | `\(N-1\)` | | | ### Hipótesis $$ `\begin{cases} H_{0}: \mu_{i} = \mu_{j} \\ H_{1}: \mu_{i} \neq \mu_{j} \end{cases}` \forall i \neq j $$ --- ## ANOVA .panelset[ .panel[.panel-name[R base] ```r aov(data = penguins, formula = body_mass_g ~ species) %>% summary() ``` ``` Df Sum Sq Mean Sq F value Pr(>F) species 2 146864214 73432107 343.6 <2e-16 *** Residuals 339 72443483 213698 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 2 observations deleted due to missingness ``` ] .panel[.panel-name[report] ```r aov(data = penguins, formula = body_mass_g ~ species) %>% report() ``` ``` The ANOVA (formula: body_mass_g ~ species) suggests that: - The main effect of species is statistically significant and large (F(2, 339) = 343.63, p < .001; Eta2 = 0.67, 90% CI [0.63, 0.71]) Effect sizes were labelled following Field's (2013) recommendations. ``` ] .panel[.panel-name[report as table] ```r aov(data = penguins, formula = body_mass_g ~ species) %>% report() %>% as.data.frame() ``` ``` Parameter | Sum_Squares | df | Mean_Square | F | p | Eta2 | Eta2 90% CI ----------------------------------------------------------------------------------- species | 1.47e+08 | 2 | 7.34e+07 | 343.63 | < .001 | 0.67 | [0.63, 0.71] Residuals | 7.24e+07 | 339 | 2.14e+05 | | | | ``` ] ] --- class: inverse, center, middle # No `report` <img src="https://media2.giphy.com/media/hyyV7pnbE0FqLNBAzs/200.webp?cid=ecf05e47tm6f3m9fpzck6mm3jh3c50u40hfkxjxnua0x962s&rid=200.webp" width="50%"> --- class: inverse, center, middle # Using `report` <img src="https://media2.giphy.com/media/l0amJzVHIAfl7jMDos/200.webp?cid=ecf05e47tm6f3m9fpzck6mm3jh3c50u40hfkxjxnua0x962s&rid=200.webp" width="50%"> --- class: inverse # Gracias por su atención!! .pull-right[.pull-down[ ### <i class="fa fa-paper-plane" role="presentation" aria-label="paper-plane icon"></i> carlos221296@gmail.com ### <i class="fa fa-link" role="presentation" aria-label="link icon"></i> [carlostorrescubila.github.io/](carlostorrescubila.github.io/) ### <i class="fab fa-twitter" role="presentation" aria-label="twitter icon"></i> [@carlos_tc22](https://twitter.com/carlos_tc22) ### <i class="fab fa-github" role="presentation" aria-label="github icon"></i> [@carlostorrescubila](https://github.com/carlostorrescubila) ]]